高校数学 式と証明「実数の2乗は0以上」の使い方 式と証明不等式の証明で相加平均と相乗平均の大小関係を使うコツ 式と証明相加平均と相乗平均の等号成立条件 式と証明相加平均,相乗平均 式と証明複雑な式の因数分解 部分分数分解の公式とやり方を解説! あなたは部分分数分解を単なる「式の変形」だと思い込んでいませんか? 実は数学b の数列の単元や数学3の積分計算でとてもお世話になる、大切な式変形なんです。 今回は、その「部分分数分解」を、公 15公式 二つの数列について次の公式が成り立つ。 足し算やかけ算をしてから極限をとった値と、極限をとって足し算やかけ算をした値が一致します。この性質を使ってさまざまな数列の極限を求めることができます。 問題

極限 微分 高校数学の美しい物語
リミット 数学 公式
リミット 数学 公式-極限で初めて出てきたリミットには、分配法則のような性質があります。 しかし、その分配法則が成り立つのは、 収束する時のみという制限 が設けられています。リミットは英語で"限界・極限"を意味する単語です。 リミットの下の"x→1"は、"xの値を限りなく1に近づける"ことを意味しています。 "xの値を限りなく1に近づける"ことから、"極限値"という言葉ができているんですね。 は、「xを1に限りなく近づけたとき、 (x+2)の値は何に限りなく近づいていくか」を表した式です。 "x=1"を代入すると、"x+2=3"なので、 "x+2"は



数列の和の極限
数列の極限 項が限りなく続く数列を無限数列という.無限数列 {an} { a n } で n n が限りなく大きくなるとき, an a n が一定の値 α α に近づくならば, {an} { a n } は α α に収束するといい, α α を極限値という.記号では lim n→∞an = α lim n → ∞ a n = α またここで実際に極限分野で最重要公式の一つである lim x→0 sinx x = 1 lim x → 0 sin x x = 1 の関数の f (x) = sinx x f ( x) = sin x x で実際に考えてみましょう。 まずこの関数の定義域を考えます。 分母にxがある時点で、「分母に0がきてはいけない」っていう 高校数学微分 リミットh 0 E H 1 H 1をもとにして次の極限値 高校数学 極限 Limit について 1 練習編 映像授業のtry 三角関数の極限の公式 Lim X 0 Sin X X 1 Irohabook
これを数学的な式で表すと、 ①式の前に書かれている記号はリミットΔxテンド0と読み、①式においてΔxを限りなくゼロとした時の極限値を求めるものである。 具体例として図8の曲線でもある、f(x)=x 2 の場合を考えてみよう。 a \leq x \leq b a ≤ x ≤ b において連続な関数 y = f ( x) y=f (x) y = f (x) に対して, lim n → ∞ b − a n ∑ k = 1 n f ( a ( b − a) k n) = ∫ a b f ( x) d x \lim_ {n \to \infty}\dfrac {ba} {n}\sum_ {k=1}^n f\left (a (ba)\dfrac {k} {n}\right) =\int_a^b f (x)dx n→∞lim nb− a1: lim x → 0 sin x x = 1 教科書に載っている非常に基本的な公式です。 三角関数の極限はほぼこの公式がもとになっています。 2: lim x → 0 tan x x = 1 公式1から簡単に導けるので必ずしも覚えなくてもよいです。
収束せず正の無限大、負の無限大、振動することを 発散する という。 極限を表す記号として、lim (英語:limit, リミット、ラテン語:limes)という記号が一般的に用いられる。 例えば次のように使う lim n → ∞ x n {\displaystyle \lim _ {n\to \infty }x_ {n}} lim x → 0 sin x x = 1 {\displaystyle \lim _ {x\to 0} {\frac {\;\sin x\;} {x}}=1}極限計算機で関数の極限を計算します。片側、両側の極限もサポートされています。極限が計算されるポイントは、たとえばπ/ 4 のような数字または単純な式で指定することができます。極限の計算は正の無限大( inf)、負の無限大( minfリミットの関連情報 記号 \(\approx\) は「ほぼ等しい」という意味です。 例えば、次のようになります。 \ \begin{aligned} ( t \Delta t )^2 &= t^2 2t \Delta t (\Delta t)^2\\ &\approx t^2 2t \Delta t \end{aligned} \ これを承知しておかないと、突然項が消えて式が追えなくなったりしますので、覚えておくといい
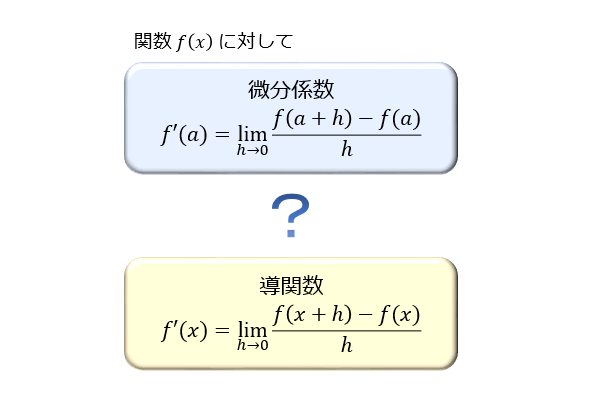



微分係数と導関数の違いとその使い分け アタリマエ
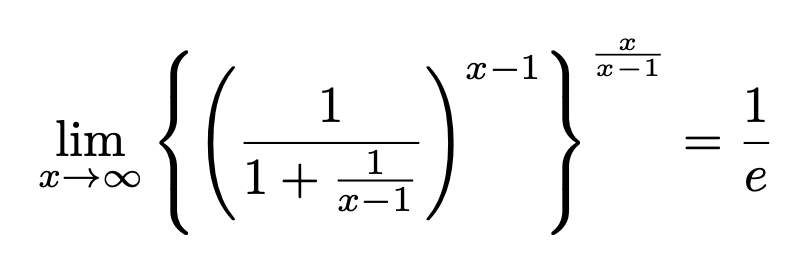



極限公式で覚えておくべきはたった3つ 証明 導出 覚え方を教えます 東大医学部生の相談室
極限値の計算法則について説明しましょう。 カッコでくくられているものは分解ができます。 関数f(x)と切り離せる定数kは、式の一番まえに持ってくることができます。 1つのリミットでくくられた極限値は、分解することができます。Search the world's information, including webpages, images, videos and more Google has many special features to help you find exactly what you're looking for 分母も分子も無限大に発散する場合の極限の考え方 基本数列の極限の性質で見たように、数列 $\{a_n\}$, $\{b_n\}$ が収束し、極限値を $\alpha$, $\beta$ とすると、\ \lim_{n\to\infty}\frac{a_n}{b_n}=\frac{\alpha}{\beta} \となることを見ました。その際、「これが成り立つのは収束するときだけであり、発散




極限公式の本質 証明 使い方を徹底解説 大学受験数学の解き方




微分係数とは 見やすい図で誰でもすぐわかる 定義や求め方も 高校生向け受験応援メディア 受験のミカタ
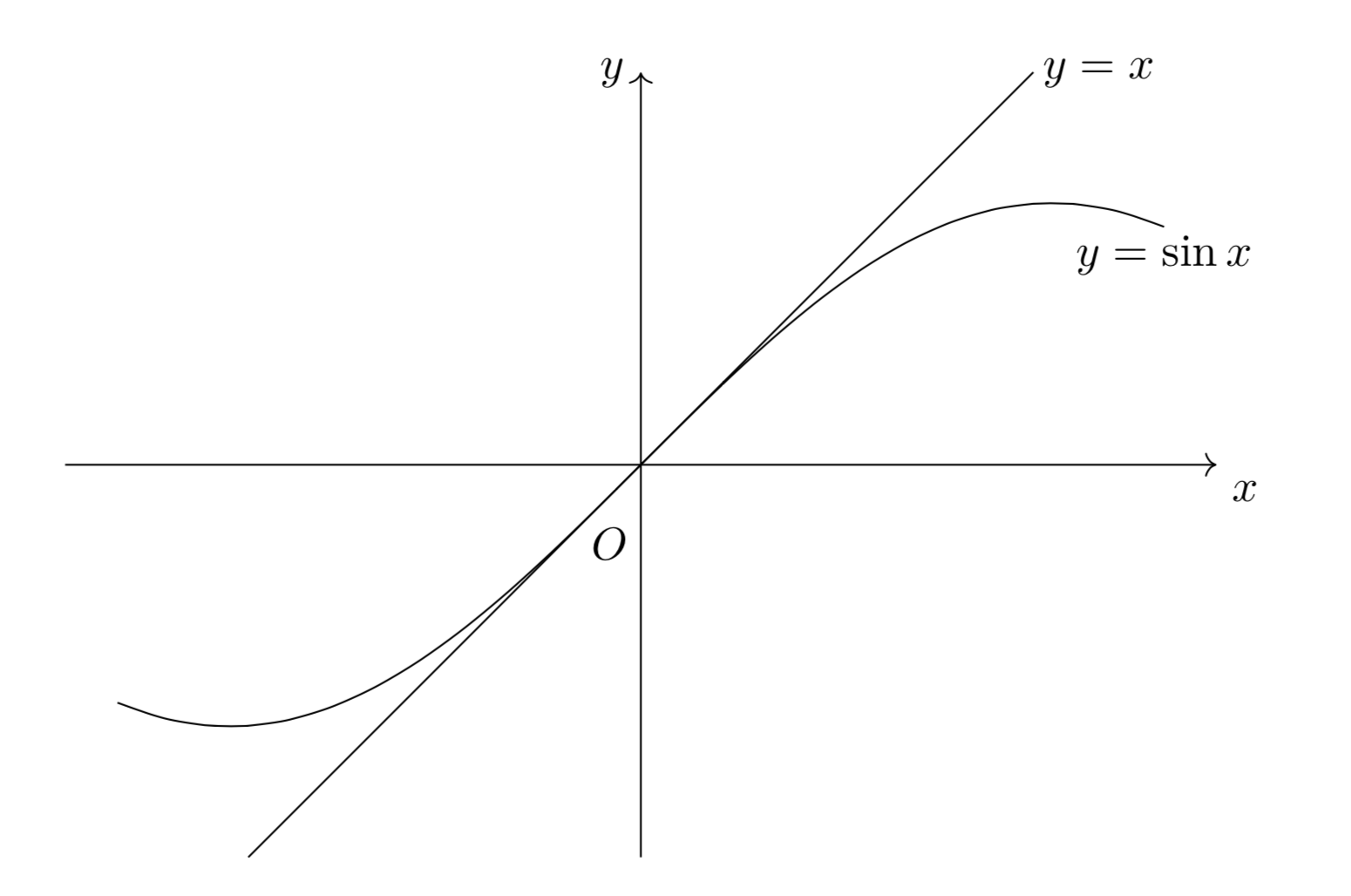
第6章では「微分法・積分法」という新しい分野に入ります。 まずは 「極限 (limit)」 について学習していきましょう。 関数f (h)における 極限値 とは、hがある値にどんどん近づいていくときのf (h)が近づく値を指します。 例えば、hが0に近づくときの極限値は次のように表せます。はさみうちの原理 数学Ⅲ 数学的帰納法 証明 関数の発散の速さの順序とその証明を分かりやすく解説!(極限のコツ) 指数関数や対数関数、xの整式、階乗など関数の極限が発散するはやさの順序を紹介し、例題を通して証明をしていきます。三角関数の極限の公式は数学Ⅲで最も重要な公式の一つです。 三角関数の極限の公式は x が 0 に近づくと sin x と x の差がなくなっていくことを示しています。 例 sin 5x を x で割った分数の極限値は、次のように 5x を分母につくって求めます。



対数関数 分数 極限




指数 対数関数の極限 と応用公式 2つの不定形と4つの極限公式だけ覚えよう 青春マスマティック
関数の極限③:片側極限 (左側極限・右側極限)と極限の存在 関数の極限④:指数関数と対数関数の極限 関数の極限⑤ 三角関数の極限の公式 lim sinx/x=1、lim tanx/x=1、lim (1cosx)/x²=1/2 関数の極限⑥:三角関数の極限(基本) 関数の極限⑦:三角関数の極限(置換) 関数の極限⑧:三角関数の極限(はさみうちの原理) 極限値から関数の係数決定 オイラーとヴィエト lim n → ∞ 1 n ( f ( 1 n) f ( 2 n) ⋯ f ( n n)) = ∫ 0 1 f ( x) d x \lim_ {n \to \infty} \dfrac {1} {n} \left (f\left (\dfrac {1} {n}\right) f\left (\dfrac {2} {n}\right) \cdots f\left (\dfrac {n} {n}\right) \right) = \int_0^1 f (x)dx n→∞lim n1ポイント 三角関数の極限 lim x→0 sinx x = 1 lim x → 0 sin x x = 1 lim x→0 x sinx = 1 lim x → 0 x sin x = 1 重要公式です.結果のみを丸暗記で構わないのですが,なぜこの極限が1に収束するかを説明できないと,本当に極限や微分を理解しているとは言えませ



数学極限公式が覚えられない 自分は暗記が苦手で極力暗記をし Yahoo 知恵袋




高校数学 F A は接線の傾き 映像授業のtry It トライイット
リミットサイクル リミットサイクルの概要 ナビゲーションに移動検索に移動 ファン・デル・ポール振動子で現れる安定なリミットサイクル。内側の軌道も外側の軌道も、ある閉軌道に漸近している。リミットサイクルは非線形系でのみ現れる。リミットサイクルと高校の数学では,無限大の厳密な定義(εδ論法)を要求しませんので を証明せよとは言いません. であって,かつ だから とするまでです. 同様にして,無限大になる式の定数倍も無限大になります. ただし,符号が逆の場合は負の無限大になります. The latest Tweets from 公式遊戯王OCG (@YuGiOh_OCG_INFO) 遊戯王OCGの商品やイベント等の最新情報をお知らせする遊戯王OCG公式




数列 1 1 N N が収束することの証明 再掲載 身勝手な主張




極限での等号 とは Yoshidanobuo S Diaryー高校数学の 思考 判断 表現力 を磨こう ー
第1章 微積分(数学II)の落ち穂拾い 11 微分の応用 P03 合成関数 合成関数の微分 積の微分 12 回転体の体積 P06 x 軸中心の回転体概要 ポアンカレ・ベンディクソンの定理は次のような事を示している。二次元平面上の連続力学系に於いて任意の状態空間におけるコンパクト部分集合にとどまる軌道は 固定点、周期軌道、有限個の固定点からなる連結空間のいずれかである。 together with homoclinic and heteroclinic orbits connecting these数式ツールには数多くの数学記号が用意されています。そのうち高校数学で頻繁に用いるものを以下に まとめました。 演算子・関係子 出力 キー入力 等号= = not equal≠ ¥ne または ¥neq 不等号≥ 環境による。 >= または 日本語入力で『>』を変換 不等号≧
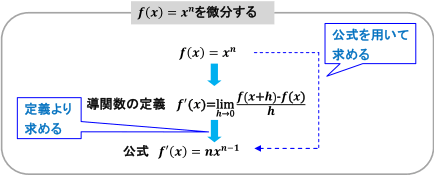



導関数と微分 数学 苦手解決q A 進研ゼミ高校講座



極限とは 公式一覧や極限計算のポイントをわかりやすく解説 受験辞典
この記事を読むとわかること ・高校数学において極限公式は3つだけ覚えてれば十分! ・極限公式の覚え方 ・その他の極限公式の導出のしかた ・極限公式の証明方法 目次 1 大学受験数学で覚えておくべき極限公式は?11 極限公式は3つだけ覚高校数学で必要な公式および重要な関係式を項目毎にまとめています. 2次関数 数と式 複素数と複素平面 行列 三角比 三角関数 指数と対数 lim x → 3 ( x 2 2 x − 3) lim x → 1 x 2 − 3 x 2 x − 1 (1) x → 3 のとき, x 2 2 x − 3 は 3 2 2 ⋅ 3 − 3 = 12 に近付く. したがって, lim x → 3 ( x 2 2 x − 3) = 12 である. (2) x 2 − 3 x 2 x − 1 は となるから, x → 1 のとき 1 − 2 = − 1 に近付く. したがって, lim x → 1 x 2 − 3 x 2 x − 1 = − 1 である. (2)では




負の無限大への極限対策 怜悧玲瓏 高校数学を天空から俯瞰する




極限の定義 公式 計算問題の解き方 高校数学 Irohabook
F'(x) と f'(a) のまとめ! f'(a) は接線の傾き;T= 1 s t = 1 s とおくと, t→0 t → 0 のとき s→ ∞ s → ∞ となる.よって,上式は e = lim s→∞(1 1 s)s e = lim s → ∞ ( 1 1 s) s と表すこともできる. e の値は, ・・・・・・・・・ e の特徴は,関係式 d dxex = ex d d x e x = e x が成り立つことである.すなわち, e e を底とする指数関数は,それ自身の導関数と等しくなる. この自然対数の底 e e のことを⑦ 数列の極限に関する公式 =a ®¥ n n lima 、 =b ®¥ n n limb のとき (n®¥のとき、,a b n n ® ® a b とも書く) (a) >a b n n Þa³b (b) ± = ± a b ®¥ n nlim( ) n a b 、 =ab n ®¥ lim a b 、 b a = ®¥ n n n b a lim (b¹0)が成立する。 ⑧ 無限等比級数= ××× ××× ¥ = å 2 1 1 1 n k k ar a ar ar ar




ロピタルの定理 Wikipedia




数列の極限について 数学 苦手解決q A 進研ゼミ高校講座
微分積分 公式導出 微分方程式 数学Ⅲ 極限 関数方程式f (xy)=f (x)f (y)型の解法とコツ (大学受験レベル) 関数方程式のうち、積分・微分方程式ではないタイプについて、有名な問題を通してその解法とコツを紹介しました。 Shu Yasuda 微分積分 数列 数学平均変化率と微分係数 (2) §2 微分法 3.平均変化率と微分係数(その2) 前の事柄を,数学的な記号を用いて表現してみましょう。 行う内容は,今までと同じです。 つまり,ある区間における変化の割合を考え(平均変化率),そして,その区間を小さく 数学 limx→a↑これってどう読むんですか?どういう意味ですか? limh→0とかも急に登場してきてどうしたら良いのかさっぱり分かりません。limx→a は、"limit as x goes to a" と読み、x を a に近づける時の極限値を表します。よって、



対数関数 分数 極限
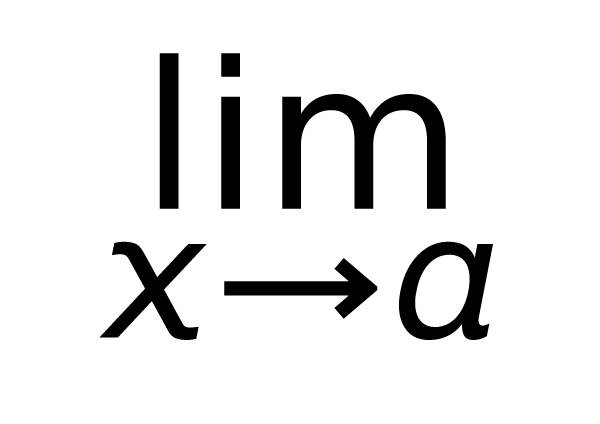



極限 高校数学入門講座 極限 きょくげん Lim リミット 数と式 大学受験講座 東京先生




数学iii 関数の極限 と 数列の極限 の2つの違い




無限数列の極限 おいしい数学




基本 対数関数の極限 なかけんの数学ノート




極限計算の本質を解説してみた 大学受験数学の解き方




極限の定義 公式 計算問題の解き方 高校数学 Irohabook




極限って何 極限のその先へ 高校数学なんちな



極限とは 公式一覧や極限計算のポイントをわかりやすく解説 受験辞典



数列の和の極限
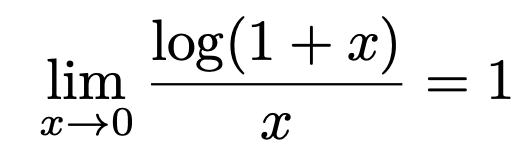



極限公式で覚えておくべきはたった3つ 証明 導出 覚え方を教えます 東大医学部生の相談室




極限の考え方を知ろう Lim リミット って一体なに




無限等比数列の極限 おいしい数学




極限の考え方を知ろう Lim リミット って一体なに



数列の和の極限




微分係数の極限値を求める時に分数の形ではカッコをつけないのにlim A B などの形 Clear




高校数学 関数の極限 三角関数の極限 置換 受験の月




平均変化率と微分 微分係数との関係をわかりやすく解説 ネットdeカガク




極限の定義 公式 計算問題の解き方 高校数学 Irohabook




数 三角関数の極限公式の証明 理系のための備忘録




高校数学 数列の極限の性質 問題編1 映像授業のtry It トライイット




片側極限の求め方がわかりません Clear




極限の定義 公式 計算問題の解き方 高校数学 Irohabook




極限 極限公式の利用 大学受験数学 Youtube
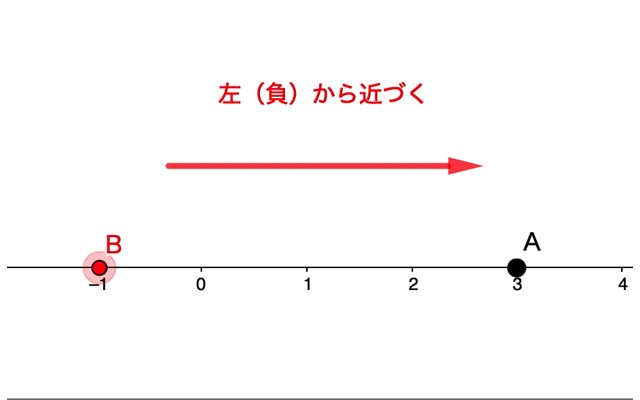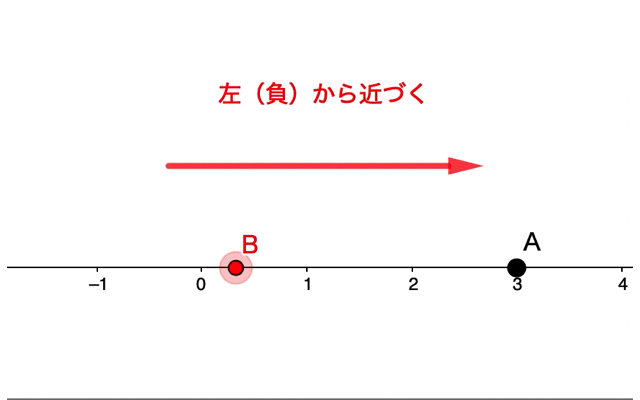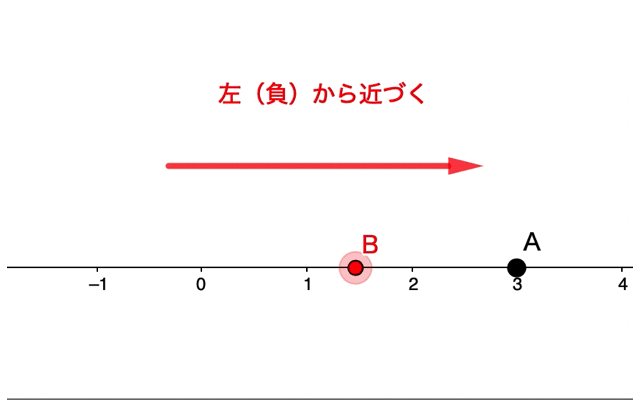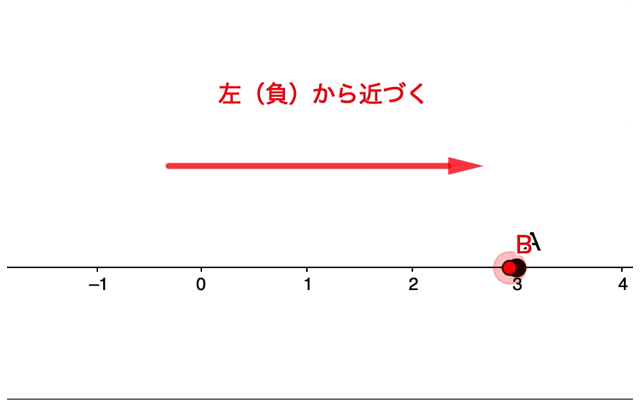



超簡単 極限って何 数学のリミットが意味することを図的に理解してみよう 青春マスマティック




画像でわかる高校数学bot 極限 三角関数の極限 T Co J6txuwpx39




微分係数とは 見やすい図で誰でもすぐわかる 定義や求め方も 高校生向け受験応援メディア 受験のミカタ




極限値とは 数学ii By Okボーイ マナペディア




極限の定義 公式 計算問題の解き方 高校数学 Irohabook



3




高校数学 定積分で表された関数の極限 Lim1 X A F T Dt 受験の月




極限 微分 高校数学の美しい物語
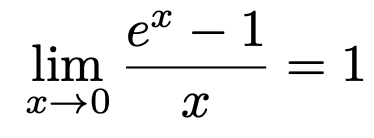



極限公式で覚えておくべきはたった3つ 証明 導出 覚え方を教えます 東大医学部生の相談室



極限値の絶対値がわかりません 0と 0の違いってなん Yahoo 知恵袋



1




高校数学 極限 Limit について 2 練習編 映像授業のtry It トライイット




微分係数とは 見やすい図で誰でもすぐわかる 定義や求め方も 高校生向け受験応援メディア 受験のミカタ




数列の極限に関する知識まとめ 理系ラボ



極限値の計算問題 京極一樹の数学塾




不定形の極限とは 解き方は実はたったの2つ 大学受験数学の解き方
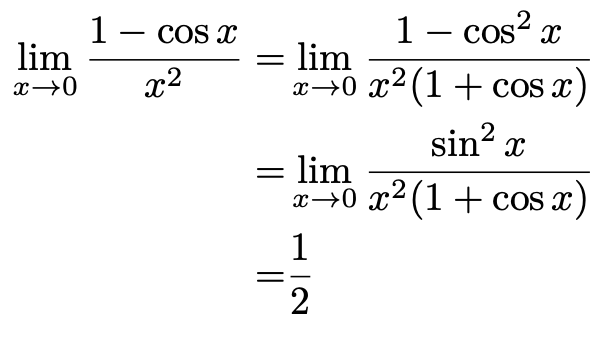



極限公式で覚えておくべきはたった3つ 証明 導出 覚え方を教えます 東大医学部生の相談室




対数関数 分数 極限
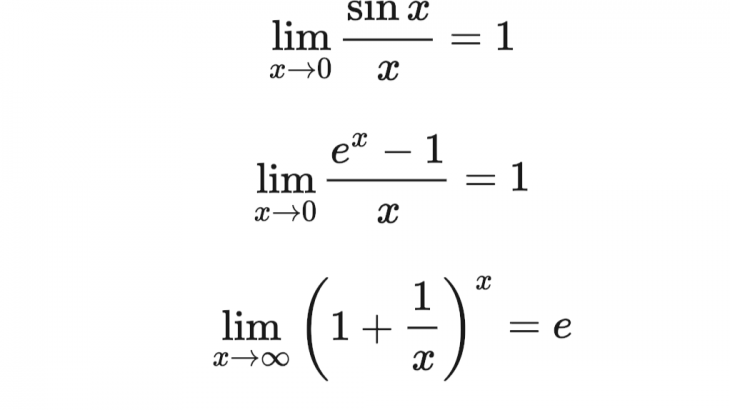



極限公式で覚えておくべきはたった3つ 証明 導出 覚え方を教えます 東大医学部生の相談室



極限値の計算問題 京極一樹の数学塾
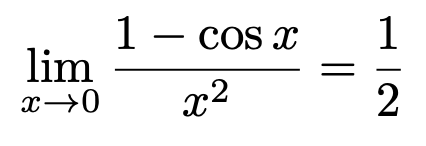



極限公式で覚えておくべきはたった3つ 証明 導出 覚え方を教えます 東大医学部生の相談室




eに関する極限公式 高校数学 Youtube




Lim 1 X 無限大となります 分母が0のときの極限の求め方を解説しました Youtube




数学 極限値からの係数決定 なんで分子が0になるの 数スタ



極限公式で覚えておくべきはたった3つ 証明 導出 覚え方を教えます 東大医学部生の相談室




高校数学 極限 Limit について 2 練習編 映像授業のtry It トライイット




公式 覚えておくべき有名な極限のまとめ 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開




高校数学 関数の極限の基本 3 問題編 映像授業のtry It トライイット




高校数学の微分公式一覧 例題と証明付き 理系ラボ




高校数学 三角関数の極限 4 問題編 映像授業のtry It トライイット




関数と極限の計算問題 解答 高校数学の知識庫




高校3年数学 数列の極限 3章関数と極限 赤城 ᴗ




極限公式で覚えておくべきはたった3つ 証明 導出 覚え方を教えます 東大医学部生の相談室



極限値の計算問題 京極一樹の数学塾




対数関数 分数 極限
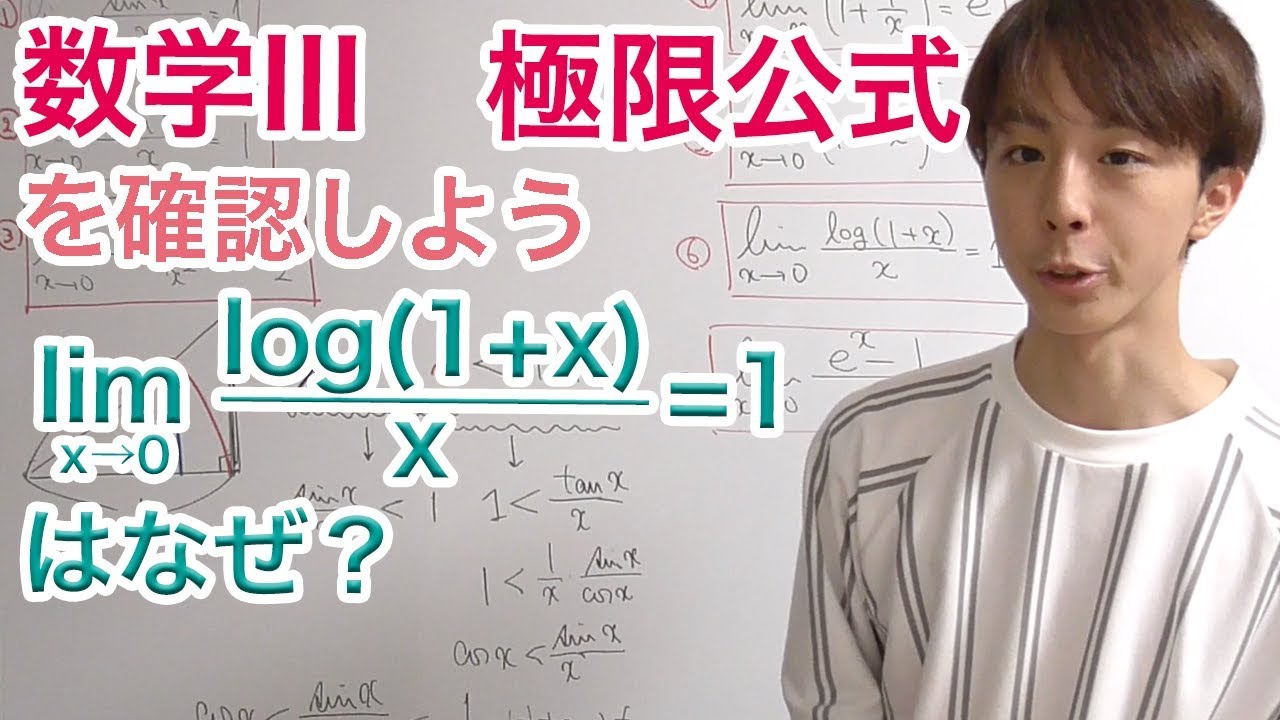



数学iiiの極限公式を確認しよう Youtube




不定形の極限の求め方と関数の極限公式をわかりやすく説明しました




多項式 指数関数 階乗の比の極限 高校数学演習 Youtube



極限とは 公式一覧や極限計算のポイントをわかりやすく解説 受験辞典




数列の極限に関する知識まとめ 理系ラボ




数学iiiの極限公式を確認しよう Youtube



極限 数学入試問題




三角関数の極限公式とその証明 おいしい数学



1




超簡単 極限って何 数学のリミットが意味することを図的に理解してみよう 青春マスマティック




数3の極限の問題です 解答だけでわかりにくいかもしれませんがお願い 数学 教えて Goo



対数関数 分数 極限




指数関数と対数関数の極限の公式 高校数学の美しい物語



対数関数 分数 極限
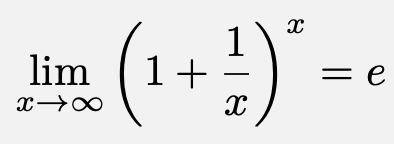



極限公式で覚えておくべきはたった3つ 証明 導出 覚え方を教えます 東大医学部生の相談室




三角関数の極限の公式 Lim X 0 Sin X X 1 Irohabook




高校数学 関数の極限 三角関数の極限 はさみうちの原理 受験の月



3




高校数学 関数の極限 三角関数の極限の公式 Lim Sinx X 1 Lim Tanx X 1 Lim 1 Cosx X 1 2 受験の月




極限公式一覧 極限のイメージから基礎問題 重要テクニックまで総まとめ 青春マスマティック



極限とは 公式一覧や極限計算のポイントをわかりやすく解説 受験辞典




きみは ロピタルの定理 を本当に知っているか Saitei Net




はさみうちの原理 Twitter Search




極限 極限公式の証明 大学受験数学 Youtube
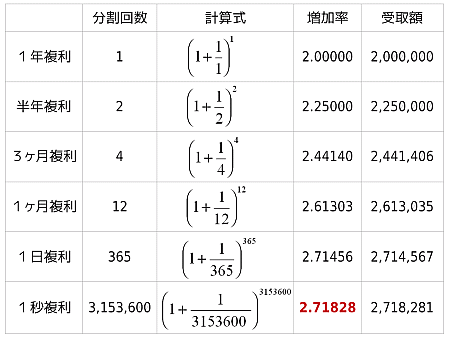



数列 連続複利とネイピア数 E 大人が学び直す数学



高校数学微分 リミット 1 H 1 H がeになるってい Yahoo 知恵袋




三角関数の極限の公式 Lim X 0 Sin X X 1 Irohabook
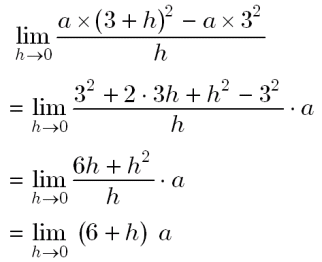



微分 瞬間の速度 極限 を使う 大人が学び直す数学




極限公式一覧 極限のイメージから基礎問題 重要テクニックまで総まとめ 青春マスマティック



0 件のコメント:
コメントを投稿